Feb 28: An AC Microphone Amplifier

AC Microphone Amplifier

Use of "Single Supply" Op Amp
-can be operated with V+ = 12 V, V- = -12 V but also can be operated with V- = GND (and output can swing all the way to V-)
-Though we don't take advantage of the single supply's "hallmark," single supply op amps allows one to work down to its negative supply (ground) 

Goal:
-Build an audio amplifier circuit
-Amplify the output of a microphone
-Drive a speaker (actually a piezoelectric buzzer)

Signal of Interest: 
-Electrical output of a microphone (with a small amplitude of 20 mV or less and is AC i.e. audio frequencies ranging from 20 Hz - 20 MHz)


1) Setting the Gain of the Audio Amplifier (Circuit #1)

Note: Configured the '358 as a non-inverting amplifier

Why? 

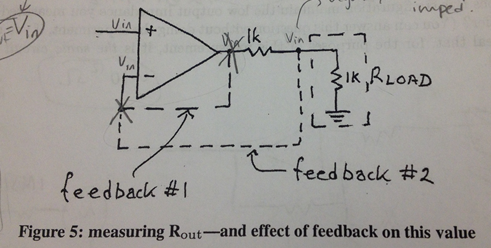
Here, a non-inverting amplifier has a low output impedance (for small signals) while the input impedance is very high, which is useful when an application requires such high input impedance

-Choosing components and values to create CKT1 to achieve reasonable gain

-Assumptions:

Audio signal of interest ~ 15 mV

Output voltage in range 0-3.5 V (since powering amplifer with +5 V and '358 can go from ground or close to ground to about 1.5 V below the positive supply)

First, we thought about the effective resistance we'd need for CKT 1, which we calculated by using the equation for non-inverting amplifier:

Vout = 3.5 V

Vin = 15 mV = 0.015 V

So: 3.5 V = (1 + (1 M/R_ckt1))* 0.015 V

R_ckt1 = 4303 Ohms or about 4.3 kOhms

To check/review, we used the Golden Rule #1, which says:

Vin = V- = 0.015 V = (R_ckt1/(R_ckt1 + 1 M))*3.5 V

so R_ckt1 = 4.3 kOhms

Then, we thought about how to have a range of output voltage from 0-3.5 V and thought we could use a potentiometer. To get the right effective resistance, we needed a 10 k pot and R1 and R2 values that produced an effective resistance of 4.3 kOhms.

Our initial idea of CKT1 to get the right effective resistance AND to have variable resistance to have a range of output voltage values

However, we soon realized that we had forgotten to consider gain (our input voltage is only about 15 mV so we needed to amplify the signal).

Thus, we took the ratio of the amplitude of output voltage over input voltage = (3.5/2) / 0.015 = 100

and decided we wanted a gain of about 100 (up to 100 or else above 3.5 V)

Then, using the gain factor for non-inverting amplifiers, we determined R_ckt1 again:

1 + (1 M / Rckt_1) = 100

Rckt_1 approx = 10 kOhms

We tested combinations of resistors and potentiometers that satisfied this R_ckt1 requirement and decided on:

R_pot = 10 k

R2 = 10 k 

And got rid of R1

so now:

because R_pot can be adjusted from 0 to 10k which means our range of resistance would be from 10 k to 20 k (G=100 to G<100 satisfying our upper limit for gain)

*Later changed R2 = 6.8 k because our actual gain wasn't high enough (so output signal not large enough)  (Mentioned in detail later)

We later realized we took care of volume control by adding the potentiometer.

And by considering the max gain to be 100 and using appropriate components and values to upkeep that requirement, we were able to keep the user from making the output rail.

Clipped signal

Added buzzer to test

distorted signal after adding buzzer

To keep the signal from getting clipped below ground (have room for voltage swings), we had to make the audio signal ride on a DC level. We ultimately wanted the DC offset to pass through unaffected (G = 1) while the AC signal would have a large gain (G= 100), i.e. we wanted CKT1 to be a follower at DC but an amplifier at AC.

To achieve this, we added a capacitor to the circuit. At high frequency, C would be just like a wire, so what we had to worry about when choosing the capacitance was the lower frequency limit of 20 Hz. 

So now, considering the effective resistance:

R_ckt1 = 1/(omega*C) + R2 + R_pot = 10k

1/(2*pi*20 Hz)  = 1/(omega*C) since we had to consider the low f case.

C = 1.2 uF but we used 4.7 uF and R2 = 6.8 kOhms to increase the gain (our output signal was not strong enough)

Adding a Microphone

-replacing function generator with microphone to encode voice

-microphone includes a high input impedance FET

During silence, Vout = 5V because no current flow in circuit

Video of us looking at our voices on the scope

Connecting Microphone to Amplifier

-Microphone a +5V DC signal with a small (~20 mV) AC signal on top so need an intermediate circuit between the microphone and amplifier (CKT#2)

CKT#2 Requirements:

1) block large DC voltage from microphone but pass AC signal

2) make AC audio signal ride on a ~1.75 V DC offset so that the audio signal lies in the middle of the output range of amplifier

-want Zin of second subcircuit to be much larger than Zout of previous stage and also not waste power

Our idea for CKT2:

We want:

Zout,micro << Zin, ckt2

-so we want Zin, ckt2 = R1 || R2 to be relatively large

and 

Zout, ckt2 << Zin, op amp 

where Zout, ckt2 = R1 || R2

-The second condition should not be difficult since Zin, op amp is huge (~10^12)

Also, since we want DC offset of 1.75 V, the ratio of R1 and R2 have to be such that 

1.7 = (R2/(R1+R2))* 5 

so we picked: R1 = 2.7 MOhms and R2 = 1.0 MOhms 

-This satisfied our R1 || R2 requirement (relatively large and the right ratio)

Above, we effectively created a high pass filter so our worst case was 20 Hz (low f limit). So we wanted f-3db << 20 Hz. And if R1 and R2 are too small, we'd waste power.

And since we want f-3db << 20 Hz or 1/(RC) << 20 Hz (lower f limit in our case),

C has to be less than 2.5E-5 F so we picked a capacitor with capacitance in the uF. 

So our circuit looked like:

Feb 26: Op Amp (Part II)

Op Amp Current Source

Looking at the current through the variable resistor (R2):

Following the Golden Rule, V- = V+ = Vin.

Using Ohm's Law: I1 = V-/R1 which must equal I1 using Golden Rule (#2) since current doesn't go through inputs of the op amp. 

So: I2 = V-/R1. 

Here, the current flowing through R2 is independent of value of R2 over a wide range of resistances, which means this is a good (relatively constant) current source as the resistance of the load changes (vs. voltage source e.g. batteries which are good at maintaining a constant voltage across a load resistor independent of the load's resistance).

Op Amp Current Source, Experimentally (8-5)

Vin  = (1k/(15k + 1k))*12 V = (1/16)*12 V = 0.75 V = V+ = V- (Golden Rule)

V- = IR 
0.75 V = I (180)  --> I = 0.004 amps or 4 mA

Observations:
-When R-load = 0 Ohms, configuration like a follower. 
-The current was calculated to be constant at around 4 mA.
-We observed 4.2 mA using the multimeter, but as we adjusted (increased) the resistance using the potentiometer, (or when R-load) became too large (where Vout > 12 V), we did not observe this constant current behavior and instead measured lower current values. 

Note: 
-This current source has a disadvantage of requiring a "floating" load (neither side connected to ground, like our 10 k load). 
-Also has significant speed limitations, which causes problems in situations in which either output current or Z-load varies quickly. 
-But precise and stable vs. our simple transistor current source


Photo-diodes
-when light absorbed at the p-n junction of a diode, photo-current generated (reverse process to LEDs)
-Size of photocurrent approximately linearly proportional to intensity of illuminating light so a diode can serve as a light detector
-To detect, we "converted" photocurrent to voltage
-But to use a resistor (for this I to V converter), 2 disadvantages: photodiode not a compliant current source as it can only sustain about 0.5 to 2 V. Also, as voltage is allowed to develop across the photodiode, response can vary (so can't really use that linear proportionality).

Solution? 
Phototransistor
-"photodiode with gain"
-when wired, each photon received causes about 100 electrons worth of current


Op Amp Current-to-Voltage Converter

-improved I-to-V converter
-small feedback resistor used to reduce sensitivity of device
-regulates/maintains current (controlled by light)
-also have a faster response time (weakness of photodiodes) by using a different type of junction ("PIN junction" vs. p-n junction)


Current-to -Voltage Converter, Experimentally

-Used a 10 k Ohm resistor for feedback loop to lower Vout (versus a 100 k to avoid saturation)

Average Input Photocurrent (middle/halfway of peak-to-peak amplitude)

Vout = -3.44 V = -Ipd (10000 Ohms)

Ipd = 0.34 mA

Percentage Modulation

-Measured from peak to peak over middle (of peaks) to the zero line

(-3.28 V / -3.44) * 100% = 96 %

-At the summing junction, Vx = 0. (Golden Rule #1)


Summing Amplifier

-Currents through input resistor add at the summing junction and flow through the feedback resistor (also proven by Golden Rule #2, in which there is no current going into the op amp inputs).

So: I-fb = I1 + I2

-Summing junction is a virtual ground (Golden Rule #1) so:

Vout = 0V + -IfbRfb = -(I1+I2)Rfb (Ohm's Law)

Vout = -(V1/R1 + V2/R2) Rfb using Ohm's Law again

And if R1 = R2 (Say they = R), then:

Vout = -(Rfb/R)*(V1 + V2) 

Here, we see that V1 and V2 and added with a gain factor, making this a summing amplifier that also inverts the signal. 

Question: Can you design a circuit that subtracts two voltages?

Using Golden Rules, Ohm's Law, and Superposition 

I1 = (V1 - V-)/R1

I2 = (V2 - V+)/R2

If = (V- - Vout)/R3

V+ = V- (Golden Rule)

Voltage Divider

V+ = (R4/(R2+R4))*V2

Now applying superposition (adding up Vout when V1 is short and when V2 is short to get Vout of the circuit shown above):

Case 1: V2 short (i.e. V2 = 0)

Vout(a) = -V1 (R3/R1) like feedback because I1 = If where I1 = V1/R1 and If = -V_out(a)/R3 (negative value because we assumed V2 = 0 so V+ = 0 so V- = 0)

Case 2: V1 short (i.e. V1 = 0)

Here, V+ = (R4/(R2+R4))*V2           

Also, V+ = V- = (R1/(R1+R3))*Vout_b

So: Vout(b) = ((R4/(R2+R4))*V2*((R1+R3)/R1)

Using superposition, Vout = Vout(a) + Vout(b) 

so:

Vout = -V1(R3/R1) + ((R4/(R2+R4))*V2*((R1+R3)/R1)

And if R1=R2=R3=R4,

Vout = -V1 + V2 or V2-V1

Summing Amplifier as a Digital to Analog Converter

-can use an op amp to build a digital to analog converter

-let 6 V represent binary 1 and 0 V represent binary 0

-Following circuit produced analog output that is proportional to 4-bit input number

Summing Amplifier, Experimentally

-circuit above sums a DC level with the input signal

I = I1 + I2 = V1/R1 + V2/R2 = 5V/10k + 12V/22k = 1 mA

Output signal offset range: +/- 10 V

Resistance of circuit:

((1/10k)+(1/(10k+22k)))^-1 + 10k = 6875 Ohms

Vout = -(10k/6875) (5V + 12V) = -24.7 V but rails so cutoff at around +/- 10.6 V

Op Amp Limitations

-Real op amps not like idealized versions

-mild violations

so modified golden rules:

1) With negative feedback, output of op amp will try to do whatever is necessary to keep the voltage difference between inputs equal to a very small difference (called offset voltage or Vos usually about a few mV).

2) Due to their very high input impedance, inputs of op amp will sink a very small current called input bias current (I-bias usually about 3 pA)

Another limitation: small amount of output current that they can supply (for 411, at most 25 mA to a load)

Also: open loop gain "rolls off" or becomes distorted at high frequencies... so gain curve:

-This roll off affects/limits op amp's ability to respond to high f signals resulting in a limited slew rate or limited "response time"

-Slew rate defined as the maximum rate at which the op amp's output can change

Note:

-roll off in gain intentional

-output of op amp fed thru a low pass filter with a f-3db of 100 Hz

-to keep op amp stable (or else subjected to spontaneous high f oscillations which could result in stray capacitance and resulting phase shifts... after feedback unintentionally becomes positive at high f, which the modified golden rule #1 doesn't support).

Op Amp Limitations, Experimentally

Slew Rate

1. Square wave input at 1 kHz... rapid rise and fall

Measured slew rate by looking at locally linear region then took slope (delta V/delta t)

slewing up:

delta V/delta t = 1.8 V/ 139.0 ns = 1.29E7 V/s

slewing down:

delta V/delta t = 2.0 V/ 139.0 ns = 1.5E7 V/s

which agreed with 411 claim of 15 V/us 

2. Sine input (not as rapid rise and fall)

Frequency at which output waveform began to distort: 100 kHz (qualitative; harder to see than it was with square waves)

Minimum slew rate = 2*pi*A*f = 2*pi*10V*100kHz = 6.3E6 V/s 

slewing up:

4V/5.56us = 7.2E5 V/s

slewing down: 

3.36V/5.56us = 6E5 V/s

Comparable to 741's claim of a typical slew rate of about 0.5 V/us (5E5 V/s).

Slew rate for square wave input greater (makes sense because of the more instantaneous or rapid change in voltage)

Op Amp Integrator

-Recall with an RC integrator circuit,

Vout << Vin for the circuit to be a decent integrator

-Op amp integrator removes that restriction.

Vout = -(1/RC)*integrate(Vin(t)dt)

holds true for a wide range of frequencies

Problem: Op amp works so well so if input signal has even a small dc offset, the integrating circuit will integrate over time to give a very large result, leading to op amp drifting to one of the supply rails

Solution: Add a large by-pass resistor into feedback loop. The DC current will flow through the resistor and not accumulate on the capacitor, avoiding the accumulation of the small dc offset mentioned above.

Op Amp Integrator, Experimentally

-unforgiving op amp integrator esp with bias currents of picoamps or offset voltages below a mV...

-integrator above sensitive to small dc offsets (gain at DC ~100)

1 kHz square wave

Vpp = 10V

Vout = 2.56 V (peak to peak) = area of input

f = 1 kHz

Z = 1/omegaC = 1.6E4 ohms

R= C ||10Mohms = 1.6E4 Ohms

Vout = (-1/(RC))*(0.5*delta t* height in V of one square in square wave), where delta t = period .... because impedance of capacitor is frequency dependent so Vout also freq or time dependent.

Using these equations, we were not able to get close to the experimental value, but we will work on this!

UPDATE/Corrected:

Our 1kHz square wave experiment worked as expected because the output voltage (peak to peak) should equal the area of one of the "squares" (since area of one "segment"/half of the triangle, which makes another (right) triangle corresponds to one of the squares of V-input.)

So: 

Vout = -1/(RC) * Area of square

Vout,calculated = (-1/RC) * 0.5 * (1/1kHz) * 5 V = -2.5 V.

(https://myclassbook.files.wordpress.com/2014/01/op-amp-integrator-waveforms.jpg)

Feb 20: Operational Amplifiers

Operational Amplifiers

-Used for amplifying signals 

ex.) microphone and speaker
Microphone (high output impedance) vs. speaker (low input impedance) so the already small voltage by microphone further attenuated

Output Impedance 
-a measure of device's ability to provide current to load
-so lower the output impedance of source, better its ability to supply current to a load
-Summary: when load connected to source, output impedance of source must be smaller than input impedance of load, i.e. Zout << Zin

Output voltage
Vout = Gain * Vin, G = gain of voltage 


Differential Amplifiers
-to measure difference between two input signals
-minimizes unwanted "pickup" of signals:

So, here: Vout = G(V+ - V-)

Characteristics of an Ideal Differential Amplifier:

-large gain

-zero common mode gain (ideally, V+ = V- (golden rule which will be mentioned later). In other words, if two input nonzero identical voltages --> expect 0 V at output)

-large (infinite) input impedance and small (zero) output impedance. Again, Zout << Zin.

Operational Amplifiers

-class of amplifiers that almost follow the aforementioned characteristics and behaviors

-require both positive and negative power supply

-We used 12 V (-12 V and 12 V) supply, but what we amplify is the difference between the two input voltages (non-inverting (+) and inverting (-)). The difference is ideally very small, but the gain factor is so large that the signal is able to be amplified to a significant (usable) amount.

Open Loop Gain of an Op Amp, Experimentally (Lab 8-1)

-Decoupling: decoupled power supplies (12 V) with small ceramic capacitors (0.1 uF) placed as close to op amp as possible to keep power line constant locally (and avoid "parasitic oscillations"). If placed further away, other high frequency along the way may interfere with stability of power supply. 

Our circuit

-Used a 10 k potentiometer to vary the resistance

-When applied 0 V, got 12 V as output (because we can't get exactly 0 V, and even a small difference in input voltage gets amplified because of the large gain).

-The 411 specification claimed "Gain = 200 V/ 1mV", meaning 1 mV of input would result in 200 V of output (or proportional to that), but we couldn't get 200 V as output because we "hit" the rail (+12V/-12V power lines).

Feedback

-"feeding" some portion of output back into input of system

-positive vs. negative feedback

• positive feedback: output fed back to reinforce input 
• negative feedback: output fed back to partially "cancel" some of input; correcting influence to stabilize system (though this decreases the gain).

Op Amp Golden Rules

-Assume negative feedback.

1) With negative feedback in place, output of op amp will do what is necessary to keep voltage difference between inputs equal 0

i.e. V+ approx = V-

ex) Suppose V- begins to drift slightly before ground (so V- - V+ < 0). The output (Vout = -(R2/R1)*Vin) will generate positive voltage, which some is fed back to input and effectively raises V- back closer to ground.

2) Due to their very high input impedance, inputs of an op amp will neither "source" or "sink" appreciable currents. 

i.e. op amp does not draw any current

Inverting Amplifiers

-inverts and amplifies signal

How?

By Golden Rule #1: V+ = V- = 0 

(V+ = 0 because non-inverting input at ground, and by the rule, V+ - V- = 0).

Then, using Ohm's Law, Vin/R1 = I1

Golden Rule #2: I1 = I2 (no current going through inputs of op amp)

By Ohm's Law again:

Vout = 0 - I2*R2 = -(Vin/R1)*R2 

or Vout = -(R2/R1)* Vin

where Vout is inverted and is amplified by a gain factor of R2/R1.


-Even though Vout may theoretically be very large, the output swing is limited by the supply voltages. Max output voltage about 1 V less than the positive supply voltage and minimum output voltage about 1 V greater than the negative supply voltage. 

-Input impedance of inverting op amp configuration:
Zin = Vin/Iin = R1

Why?
Note the virtual ground on the circuit above. The feedback in this circuit keeps that node at 0 V (mentioned before when discussing negative feedback. Tries to keep Golden Rule #1). So the input voltage would be expressed as R1 * I1, in which R1 is the input resistance/impedance.
*Note that the op amp itself has a very high input impedance (Rule #2) so this configuration may not be the best if one needs a high input impedance.


Inverting Amplifier, Experimentally

Theoretical Input: 1 V

Theoretical Output: -10 V (because R2 = 10k and R1 =1k)

Gain =  10 V /1 V = 10

Experimental Input: 1.20 V

Experimental Output: -9.6 V

Experimental Gain: 9.6 V / 1.20 V = 8 

Linearity: maintains linearity; if input a straight line, output a straight line (so no differentiating, etc.) 
(shown by triangle wave)

Frequency Effects?
-At high frequencies (we tried 3 MHz), there was no amplification, and we also observed a phase shift.

Driving circuit again with 1 kHz
-Measured input impedance of this amplifier circuit by adding a 1 kOhm resistor in series with the input.
-Created a divider (without output signal inverted):

 where R1 = 1 kOhm

So: Vin = 1 V and Vout = -4.9. (The gain was cut in half: 5 vs. 10.)
This implied: R = 1.3 kOhms

Trying to Measure Output Impedance
-No blocking capacitor needed because resistor has very low resistance
-Zout very low
-We used a 1 Ohm resistor in series with op amp output--> Vout = 10 V
Without the resistor --> Vout = 10 V
-This shows that even with a low resistance resistor (1 Ohm), most of the voltage is dropped across the load, meaning the output impedance of this circuit is VERY low.

Non-Inverting Amplifier

Using the Golden Rule #1:
Vin = V- = V+
(V- = Vin and by rule, V+ - V- = 0)

By Ohm's Law: I1 = V-/R1 (= Vin/R1 because V- = Vin)

By Golden Rule #2:
I1 = I2 (no current thru inputs of op amp)

so I2 = Vin/R1

Then, Vout = V- + (I2)*R2  = Vin + (Vin/R1)*R2 = Vin(1+(R2/R1))



Note:
-Output signal in phase with input signal (non-inverted).
-Again, configuration has very low output impedance (for low signals).
-Because input signal connected to input of op amp, input impedance of configuration very high (Golden Rule #2) but not as stable as inverting amplifier at high gain.

Non-Inverting Amplifier, Experimentally




Rf = 10k
Rg = 1k
So expected gain = (1 + (10/1)) = 11

Experimental Data:
Input V = 2.16 V
Output V = 22.2 V 
Gain = 22.2 V/2.16 V = 10.3

Measuring Input Impedance
-at 1 kHz by putting a 1 MOhm resistor in series with the input

-We placed the probe at the output NOT the input because compared to the large input impedance, the resistance of the probe is lower, which means that what we would measure here would then be the 10 MOhms, the resistance of the probe not of the circuit. Therefore, we put the probe at the output, where the output impedance is lower than the resistance of the probe, meaning the output impedance would dominate. When we had input voltage of 1V, we got 11 V as the output. To find the f-3dB point, we looked for the frequency where the output voltage became 0.707 times its maximum, which was 7.7 V. We put the probe at the output because we can't technically measure the 3dB point at the input because of the relatively low resistance of the probe (vs. the input impedance of the circuit). So, the f-3dB was 28.4 kHz, which we used to calculate Cin (omega = 1/RC so C = 1/(R*omega)), which was 5.6 pF. Then, at 1 kHz, the output impedance was calculated to be (Z = 1/omega*C, where omega = 1 kHz) 2.84E7 Ohms or 28 MOhms. 


Op Amp Follower
-like considering non-inverting amplifier when R2 --> 0 and R1 --> inf (with gain of 1)
-called a follower because output signal a replica of input signal ("follows" whatever input is doing)
-this configuration has a very high input impedance and low output impedance. Thus, it acts as a buffer between the source and load, which makes it easier for the source to drive the load without attenuation.
In other words, if we add a load to the output of the follower, the source can drive the load with minimal attenuation because the follower is like the non-inverting amplifier without the resistors.
-nearly ideal follower but not able to supply large currents


Op Amp Follower, Experimentally

Its Zin and Zout are identical to those of the op amp non-inverting amplifier without amplification (because gain = 1).

Output Impedance
-really small
-Why is it so small? due to feedback
-Tried adding a 1 kOhm resistor in series with the output of the follower

Trials:

1. Feedback #1 without load --> no change in signal

2. Feedback #1 with load --> essentially 2 kOhms outside the input --> R-load = 2kOhms --> signal cut in half

3. Feedback #2 without load --> no change in signal because all of voltage drop to load --> Rth very small

4. Feedback #2 with load --> no change in signal --> all of voltage drop to load --> Rth very small

These trials show that the output impedance is very low due to the feedback. Even after adding the 1 kOhm resistor (not load), if it's "inside" the configuration (with feedback loop around it), there would be no change in signal, implying almost all of the voltage drop is across the load.

                                     Trials 1, 2, 3                                    Trial 4